FIMMPROP

Fiber Bragg Gratings (FBGs)

3D simulation of transmission and reflection spectra with FIMMPROP software

We will show here how FIMMPROP can be used to model fiber Bragg gratings. We will study three different geometries, and use FIMMPROP to generate transmission and reflection spectra in each case for different mode orders.

FIMMPROP is a very efficient tool for the modelling of optical fiber devices. It can take advantage of the two fully vectorial fiber solvers available in FIMMWAVE and can model continuously varying optical fiber devices, such as sinusoidal fiber Bragg gratings and fiber tapers, as well as discontinuous optical fiber devices such as discrete fiber Bragg gratings, coupling between e.g. a fiber and a planar waveguide and cylindrical MMI couplers.

In this example, FIMMPROP was used to model various first-order (lossless) fiber Bragg gratings. FIMMPROP can model such devices very efficiently and accurately:

• Different mode solvers optimised for cylindrical geometries can be used to calculate the modes in the optical fibre, allowing you to perform a benchmark between different independent methods.

• For this device we relied on FIMMPROP's EigenMode Expansion (EME) algorithm to model each grating. FIMMPROP's EME uses a scattering matrix approach, which makes FIMMPROP extremely efficient to simulate periodic structures: the modes and scattering matrix for the periods are only calculated once, and the scattering matrix of the period is then multiplied by itself N times to obtain the scattering matrix of a periodic section with N periods. 

• The fully bidirectional algorithm will inherently account for all internal reflections, without having to use iterative techniques.

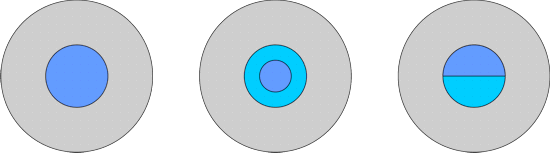
Geometry of the Fiber Bragg Gratings

The different cross-sections used in the three FBGs are shown below. We used FIMMWAVE's fiber waveguide editor to create the cross-sections for the first two fiber Bragg gratings which are cylindrical, and the mixed geometry waveguide editor to create the cross-sections in the third case where the cylindrical symmetry is broken.

Fiber cross-sections used in the three fiber Bragg gratings.

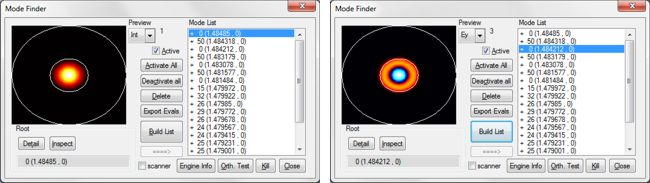
We used the FDM Fibre Solver to calculate the modes for the cylindrically symmetric designs A and B and the FDM Solver for the non-cylindrically symmetric design C. The FDM Fibre Solver uses the well-known finite-difference method to solve the vectorial wave equation in cylindrical co-ordinates, and the FDM Solver uses the same method in Cartesian co-ordinates.

These solvers are particularly well suited for this problem:

• They can take advantage of advanced techniques to improve accuracy, for instance for the modelling of features smaller than the grid size.

• They are very efficient for the modelling of structures that require a large number of modes, such as gratings: all the modes are calculated at the same time, and the solvers guarantee not to miss any modes.

• Both solvers were able to take advantage of the symmetries of the structure. For the cylindrical case, only the modes belonging to the same group of symmetry (same azimuthal order and polarisation order) as the fundamental mode were included in the simulation, as no power will be coupled to any other modes. For the Cartesian case, the symmetry settings allowed us to reduce the number of modes by a factor four. 

The number of modes and spatial resolution used by the mode solvers were optimised by performing convergence tests.

As FIMMPROP is a frequency-domain tool, the wavelength was varied using the FIMMPROP Scanner, an automated tool allowing to perform parametric scans. The scanner was used to calculate the transmission and reflection spectra into various mode orders.

Fiber Bragg Grating A - step index fibre

In this first structure, the period of the grating is made with two sections of step-index fibers with a core and a cladding.

Design of fiber Bragg grating A
(left) XY cross-section (right) YZ cross-section.

The parameters are given below.

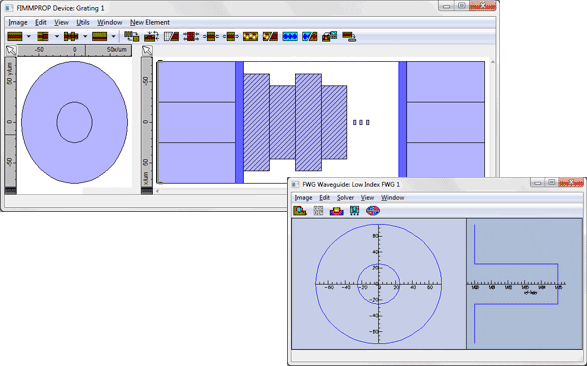
The structure designed in FIMMPROP is shown below, as well as the modes of the fibre. This structure was solved in cylindrical co-ordinates using the FDM Fibre Solver. The simulation was extremely fast; it only took 6.5s for FIMMPROP to generate the scattering matrix for each wavelength, for a device with 20000 periods!

(top-left) Fiber Bragg grating modelled in FIMMPROP with the Periodic Section,
(bottom-right) with the waveguide design in the fiber waveguide editor.

Modes of the fiber Bragg grating A calculated with the FDM Fibre Solver
(left) intensity profile of fundamental HE11 mode (right) Ey field profile of the HE12 mode

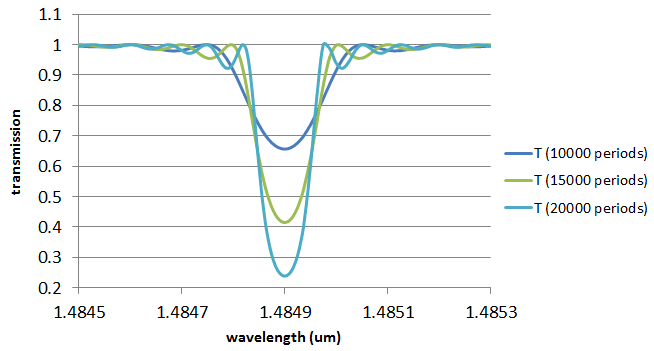
The grating includes 20000 periods. FIMMPROP's power normalise feature was used in the overlaps of the period to compensate for small numerical errors and prevent them from accumulating along the grating.

You can see below the transmission spectrum obtained with the FIMMPROP Scanner. As could be expected, only one peak is found at the Bragg wavelength of 1.4849um, where 75% of the light gets reflected.

Transmission and reflection spectrum for fiber Bragg grating A
(left y-axis) transmission (right y-axis) reflection (x-axis) wavelength in um

You can see below the evolution of the transmission spectrum when the numbers of periods is varied; a much smaller scale is used to show the detail of the peak.

Transmission spectra for fiber Bragg grating A for 10000, 15000 and 20000 periods.

Fiber Bragg Grating B - step index fibre with secondary core

In this second structure, one of the sections of the grating includes a secondary core. The structure and parameters are shown below. This structure was solved in cylindrical co-ordinates using the FDM Fibre Solver.

Design of fiber Bragg grating B
(left) XY cross-section (right) YZ cross-section.

In this case, above 50% of the light is reflected in the HE11 mode at 1.4849um, and about 30% of the light gets reflected into the HE21 mode for a slightly lower wavelength of 1.4846um. This simulation took slightly longer as further modes were needed, with a calculation time of 19s for each wavelength - still very fast!

Transmission and reflection spectrum for fiber Bragg grating B
(left y-axis) transmission (right y-axis) reflection (x-axis) wavelength in um
-
note the secondary peak showing reflection in the HE12 mode!

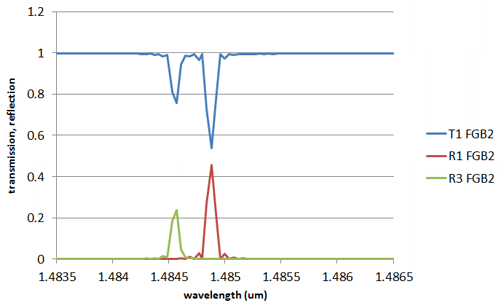
Fiber Bragg Grating C - asymmetric fibre

In this third structure, the core of one of the high-index section of the grating is modified as shown in the diagram. This structure was solved in Cartesian co-ordinates using the FDM Solver.

Design of fiber Bragg grating C
(left) XY cross-section (right) YZ cross-section.

In this case, 40% of the light is reflected in the HE11 mode at 1.4849um, and about 20% of the light gets reflected into the HE21 mode for a slightly lower wavelength of 1.4846um. This simulation only took 21s for each wavelength.

Transmission and reflection spectrum for fiber Bragg grating C
(left y-axis) transmission (right y-axis) reflection (x-axis) wavelength in um
-
note the secondary peak showing reflection in the HE12 mode!